المقدمة
إن تعليم الجبر وتعلمه وتضمينه في مناهج الرياضيات المدرسية بالشكل الذي يلبي غاية وجوده قد حظي بالاهتمام على كافة الأصعدة، فحتى وإن كان لا يوجد اتفاق تام بين التربويين حول ماهية الجبر وكيفية تدريسه المثلى إلا أن هناك أمران أساسيان متفق عليهما تماما؛ الأول ويتمثل في أهمية الجبر باعتباره بوابة رئيسية لتعلم الرياضيات بكافة مجالاتها وضرورة تدريسه عبر التطبيقات والمواقف الحياتية بعيدا عن المواقف المستهلكة الروتينية وذلك لدعم معرفة الطلبة وإتاحة الفرصة لهم للمشاركة وللتأمل وللفهم العميق، فتدريس الجبر مع الفهم العميق له نهجه الواضح من حيث المعالم والخطوط العريضة العامة، وأما الثاني فيتمثل في أن موضوعات الجبر وتعلمها تشكل صعوبة لدى الأغلبية العظمى من الطلبة.
ولا شك بأننا ندرك كمعلمين الأسباب التي ساهمت في صعوبته، وأذكر منها من واقع خبرتي كمعلمة على سبيل المثال لا الحصر معضلة وجود الفجوة الكبرى بين الحساب والجبر وعدم سدها بمشاركة الطلبة تأسيسا لتعلمهم الجبر، فهذه الفجوة فاقمت الصعوبات الطبيعية لموضوعات الجبر حتى أصبح مفهوم المتغير بحد ذاته مفهوما معزولا عن المعنى لدى العديد من الطلبة، وحتى نكون منصفين فإن الشرح النظري لفائدة الجبر ولمعنى الرمز ليس بالأمر اليسير علينا إذ أن الحديث عن الإحساس بالرموز لا يعادل الحس الرمزي الذي يخلقه الطالب نتيجة تعلمه.
ولما كان إحساس الطالب بالمفاهيم الجبرية بدءا بالرموز ضرورة أساسية لا يمكن الاستغناء عنه كان لزاما علينا أن نقيم الوضع العام للطلبة في هذا الشأن متسائلين: ما هي طبيعة الحس الجبري المأمول لدى طلبتنا؟ وإلى أي مدى يمتلكونه؟ وكيف لنا تدريسه وتعزيزه لديهم؟
إن الحس الرمزي أمر معقد، ذو أوجه متعددة وليس مفهوما محددا، فقد تناوله الباحثون بصور متعددة ولكن المعنى الجامع لتلك الصور هو خلق الإحساس لدى المتعلم بالرموز والألفة معها بحيث يصبح قادرا على استدعائها أو التخلي عنها وإجراء المعالجات عليها وقراءتها وفهم كيف ومتى ولماذا تستخدم وفقا للسياق وللموقف الرياضي.
ومن خلال قراءتي المكثفة حول موضوع الحس الرمزي وجدت أن المعنى الذي يحقق غايتي من إعداد هذه الورقة البحثية هو المعنى الشامل الذي يعكس مظاهر الحس الرمزي المتعددة، حتى نكون على دراية بمواطن الضعف والصعوبة لدى الطلبة في هذا الأمر، وقد أشار الأدب السابق إلى عدد من تلك المظاهر تمثلت بالآتي: الألفة مع الرموز، ومهارة المعالجات المرنة، ومهارة استخدام الرموز بأثر رجعي، والقدرة على فرز وفهم الرموز حسب السياق (Arcavi,1994). وانطلاقا من تلك المظاهر خرجت بتعريف الحس الرمزي على أنه ألفة الطلبة مع الرموز وقدرتهم على اختيارها وفرزها واستخدامها أو التخلي عنها بالشكل الصحيح وفي السياق الملائم.
والآن أتساءل من جديد، إن كان الحس الجبري يشكل معضلة لدى الطلبة بشكل عام فكيف الحال مع طلبة ذوي عسر التعلم! أليس من الجدير بنا كباحثين ومعلمين أن نبني ما يلائمهم من استراتيجيات تدريسية وتقويمية تساهم في بناء الحس الرمزي لديهم وتنميه وتعززه بالشكل الذي يتناسب مع قدراتهم التعلمية!
فانطلاقا من نظرتي السابقة لأهمية الحس الرمزي وضرورة تدريسه للطلبة، وإيمانا بأحقية كل طالب أن يأخذ فرصته جاء موضوع دراستي: تصميم استراتيجية تدريسية قائمة على مظاهر الحس الرمزي لتدريسه لذوي عسر التعلم من طلبة المرحلة الأساسية العليا.
الملامح العامة للاستراتيجية التدريسية القائمة على مظاهر الحس الرمزي للطلبة ذوي عسر التعلم
الفئة المستهدفة: طلبة المرحلة الأساسية العليا (السابع وحتى العاشر) من ذوي عسر التعلم في جزئية الحس الرمزي.
الموضوع: الحس الرمزي.
معالم الاستراتيجية: مهمات تدريسية وأخرى تقويمية من إعداد الباحثة قائمة على ثلاثة مظاهر رئيسة للحس الرمزي وهي (الألفة مع الرموز، المعالجات الرمزية وقراءتها، اختيار الرموز)، وتنفيذها بأساليب متنوعة تتلاءم وقدرات الطلبة وميولهم واستعداداتهم.
الأساس المعتمد: بناء الحس الرمزي للطلبة بتسلسل مناسب يتضمن تدرجا في البناء وفق توجيه منظم ومخطط له من المعلم بما يتناسب مع العسر التعلمي المحدد، حيث يوضح الطالب فهمه بالكلمات ثم له أن يربط الكلمات بتمثيلاتها شبه الرمزية تمهيدا للانتقال إلى مرحلة الترميز الرسمي مدركا الأهمية ومواطن الحاجة إلى الرموز، وبهذا يكتسب المتعلم معنى الرمز ويوظفه بمعناه الذي يشعر به وليس كمجرد رمز مجرد من المعنى.
الأدوات اللازمة: أوراق العمل، جهاز الحاسوب، مواد محسوسة، أوراق الرسم وأدواته.
معيار بناء المراحل التعليمية: تم الاستناد في بنائها إلى مظاهر الحس الرمزي التي تناولها الأدب السابق وتحديدا إلى المظاهر الثلاثة والمتمثلة بـ: (بناء الألفة مع الرموز والاختيار المناسب للرموز، المعالجات الرمزية وقراءتها).
معايير تقييم أداء الطلبة: إن الحوارات الصفية وملاحظات المعلم واستجابات الطلبة الشفوية والمكتوبة عن المهمات التقويمية المتضمنة واستدعائهم المناسب للرموز والتخلي عنها في الموقف المناسب تكشف الكثير عن مستوى امتلاك الطلبة للحس الرمزي وتعكس تطوره لديهم عبر المراحل التدريسية المتضمنة في برنامج التدخل.
والجدول (1) يوضح معالم برنامج التدخل المقترح بشكل موجز عبر مراحله الثلاث.
| المراحل التعليمية التعلمية | النتاجات التعليمية | الأنشطة التدريسية وإجراءات تنفيذها | تقويم أثر التدخل |
| أولا: المرحلة التمهيدية | · تطوير المفاهيم المسبقة من خلال إدخال العلائقية تمهيدا لاكتساب مفهوم الرمز. · تعويد الطلبة على استخدام اللغة الجبرية استنادا إلى تعبيراتهم اللفظية. |
سيتم عرضها ومناقشة إجراءات تنفيذها بشكل واضح في البرنامج المفصل اللاحق لكافة المراحل. | من خلال ملاحظة أداء الطلبة أثناء نقاشاتهم الجماعية في حل المهمة التقويمية المتضمنة في برنامج التدخل. |
| ثانيا: مرحلة بناء الألفة مع الرموز وحسن اختيارها | · تنمية قدرة الطلبة على استدعاء الرموز الرياضية أو التخلي عتها وفقا لما يقتضيه الموقف الرياضي في السياق المطروح.
· تنمية قدرة الطلبة على اختيار الرموز بالشكل الصحيح للخروج بنتائج عميقة.
|
سيتم عرضها ومناقشة إجراءات تنفيذها بشكل واضح في البرنامج المفصل اللاحق لكافة المراحل.
|
تحليل أداء الطلبة على المهمات التقويمية المتضمنة في البرنامج والتعرف على أثر التدخل في مستوى ألفتهم مع الرموز الجبرية وقدرتهم على اختيارها. |
| ثالثا: مرحلة المعالجات الرمزية وقراءتها | · تنمية قدرة الطلبة على إجراء المعالجات الرمزية وقراءة نواتجها خروجا باستنتاجات دقيقة. | سيتم عرضها ومناقشة إجراءات تنفيذها بشكل واضح في البرنامج المفصل اللاحق لكافة المراحل.
|
ملاحظة استجابات الطلبة وتحليل طرقهم في المعالجات الرمزية وقدرتهم على قراءتها أثناء تعاملهم مع المهمات |
أولا: المرحلة التمهيدية
المهمة الأولى: اشترى أحمد 3 دفاتر و 4 أقلام من إحدى المكتبات، هل لك عزيزي الطالب أن تعبر عن الثمن الذي دفعه أحمد للبائع؟ (يناقشها المعلم مع الطلبة على السبورة موظفا لغة الطالب والبناء عليها)
من المتوقع أن يستخدم الطلبة تمثيلا أوليا للمسألة يتجلى فيها التمثيل البصري كأسلوب تنظيمي لحل المسألة، فالصور هنا لها مرجعها ودلالاتها ثم بعد طرح مجموعة من التساؤلات عليهم من طرف المعلم، كأن يلفت نظرهم إلى الإحساس بمعنى السعر والتعبير عنه سينتقلون للمرحلة الثانية والتي فيها يكون الطالب رموزا ذات معنى ولكنها غير رسمية، ومع المزيد من النقاش بين الطلبة أنفسهم وبين الطلبة ومعلمهم سيقومون بعمل روابط دلالية بين الاختصارات والرموز المستخدمة ولا شك أن للمعلم الدور الأكبر في التوجيه في هذه المرحلة. وعليه فإن التسلسل المتوقع لإجاباتهم سيكون على النحو الآتي:

المهمة الثانية: (يناقشها المعلم مع الطلبة وكل منهم يجيب لوحده بتوجيه مكثف من المعلم من خلال طرح التساؤلات)
عزيزي الطالب: هيا بنا في جولة تعبيرية لنخرج معا بتعبير واحد من خلال إكمال الجدول الآتي (حيث أن محتويات العمود الأول يطرحها المعلم شيئا فشيئا ثم يتدرج معهم لينتقلوا من مرحلة التمثيل الصوري إلى مرحلة الترميز). ومن المتوقع أن تكون إجابة الطلبة كالآتي:
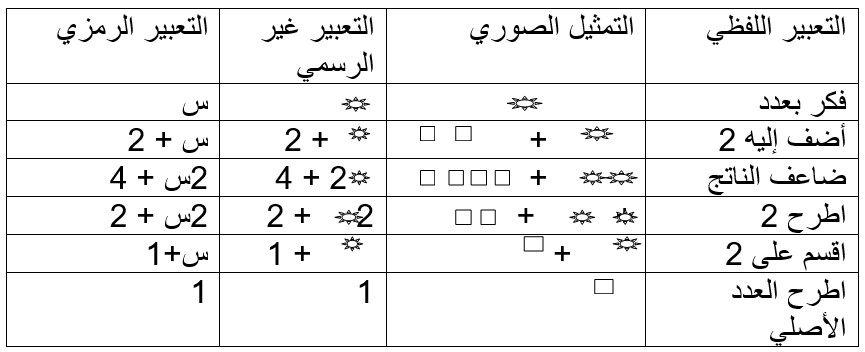
المهمة الثالثة: (مهمة فردية)
عزيزي الطالب: عبر عن المسألة الآتية رمزيا:
(أضف العدد 3 إلى عدد ما ثم ضاعف الناتج وبعد ذلك اطرح العدد 7)
ثانيا: مرحلة بناء الألفة مع الرموز واختيارها
وفي هذه المرحلة الجوهرية يسعى المعلم لبناء ثلاث قدرات لدى الطلبة وهي: (القدرة على استدعاء الرموز، والقدرة على التخلي عنها حسب طبيعة الموقف الرياضي، والقدرة على اختيار الرمز المناسب)
المهمة الأولى: (نقاشية على مستوى الصف)
وتهدف إلى بناء ألفة الطلبة مع الرموز بتعزيز شعورهم بالحاجة إلى استدعائها للتعامل مع المسألة الرياضية وهي:
ماذا يحدث لمساحة مستطيل إذا نقص طوله 10 % وزاد عرضه 10 % ؟ Arcavi,1994)).
وهناك مجموعة من الإجابات المتوقعة من الطلبة مثل: (لن تتغير المساحة، اللجوء للحسابات العددية والتجريب، …)، ويترك المعلم وقتا للنقاش بين الطلبة حتى يصلوا يقينا لحاجتهم إلى الفيصل في التقييم. وبعد هذا النقاش يتدخل المعلم ويرشدهم إلى توظيف الرموز للخروج بالحكم العام ليتوصلوا بأن:
المساحة الأصلية للمستطيل = س × ص
وبعد التغيير تصبح المساحة = (س – 10%س ) (ص + 10% ص) = 0.99 س ص
وعليه سيقتنع الطلبة أن المساحة ستنقص بنسبة 1% والأهم من النتيجة هو تعزيز شعورهم بالحاجة لاستدعاء الرموز للتعامل مع المسألة.
المهمة الثانية: (مهمة نقاشية على مستوى الصف)
عزيزي الطالب: فكر في حل المتباينة الآتية بالطريقة التي تراها مناسبة علما بأن كل الوسائل متاحة لديك كالآلة الراسمة والورقة والقلم وغيرها، لنتناقش معا في الطرق المقترحة
س – 3 > س – 6
لا شك أن كل طالب سيفكر بطريقته الخاصة والتي غالبا ما ستكون بتنفيذ اجراءات وخوارزميات من المتوقع مسبقا أنها لن توصله للنتيجة المرجوة، ولأننا نتعامل مع طلبة ذوي عسر التعلم فلربما ليس من السهل عليهم التنبؤ بأن التخلي عن الرموز واللجوء إلى استحضار مفهوم القيمة المطلقة والذي يشير إلى المسافة، ثم اللجوء للرسم مثلا وصولا للحل. ولكن ما يعنينا إتاحة المجال لهم للتمرن على الاحساس بالرموز وبالمواقف التي تقتضي استدعائها أو التخلي عنها قبل تدخل المعلم وتقديم توجهاته لهم بالنقاش والتساؤل.
المهمة الثالثة: (مهمة فردية)
أوجد قيم س التي تمثل حلا للمعادلة
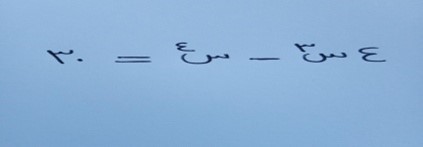
إن الحل المرجو والذي يعكس وجود الحس الرمزي هو اللجوء للرسم الهندسي باستخدام الآلة الراسمة من خلال هندسة التعبيرات الجبرية
المهمة الرابعة: (مهمة نقاشية)
أعزائي الطلبة: ماذا يمكنكم القول عن الأعداد الناتجة من طرح العدد 1 من مربع عدد فردي؟
لا شك أن اختيار الرموز له أثره الواضح في الوصول إلى الاستنتاجات الصحيحة واتخاذ القرارات المناسبة، حيث أن تمثيل العدد الفردي بالرمز ن يختلف عن تمثيله بالرمز 2ن- 1 وبإجراء سلسلة من النقاشات وحل المسألة في الحالتين سيكتشف الطلبة أن الاختيار الأمثل للرمز سيوصلهم إلى استنتاجات أكثر دقة.
ثالثا: مرحلة المعالجات الرمزية وقراءتها
وفي هذه المرحلة يسعى المعلم أن يبني لدى الطلبة قدرة جبرية تتمثل في قراءة المعالجات الجبرية والإحساس بها والخروج باستنتاجات مقنعة.
المهمة الأولى:
أعزائي الطلبة سأعرض أمامكم ثلاث مسائل على السبورة، ومطلوب منكم إيجاد قيمة س في كل منها شريطة عدم استخدام القلم والورقة، وكل ما عليكم التأمل في المسائل المعروضة والشعور بالمسائل ومحاولة التفكير في حلها لنتناقش بعد 10 دقائق من الآن بطرق تفكيركم لحلها.
والمسائل الثلاث كانت:
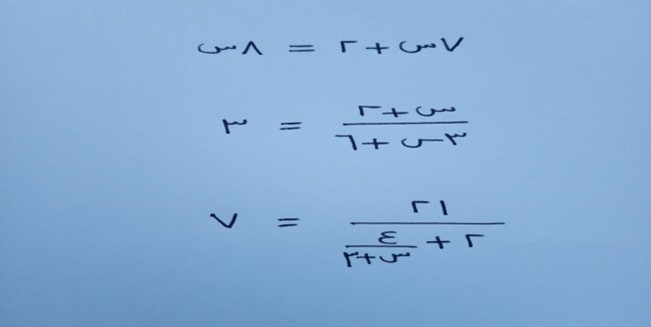
من المتوقع أن يستهجن الطلبة فكرة عدم استخدام الورقة والقلم لتنفيذ إجراءات الحل المعروفة ولكن مع إلحاح المعلم وإصراره على الشرط سيحاولون البحث عن الحل بطريقة مقنعة ومن المتوقع أن الأغلبية لن تستطيع الوصول لنتيجة صحيحة في المسائل الثلاث ولكن الغاية المرجوة هي حثهم على الخروج عن النمط الاجرائي المعتاد والمعزول عن الإحساس بالرموز والمعالجات التي تجرى عليها.
وأما ما نطمح له كمعلمين: أن يجيب أحد الطلبة عن المسألة الأولى بـ (قيمة س هي 2 لأننا لو قارننا الطرفين لتبين أن الطرف الأيسر يتضمن 8 س وهي تعادل 7س مضافا لها س أخرى وبمقارنتها بالطرف الأيمن وحذف المتشابه من الطرفين يظهر جليا أن قيمة س تساوي 2).
وأما الإجابة عن المسألة الثانية والتي تعكس وجود الحس الرمزي فتتمثل بـ (مجموعة الحل ø إذ ليس من الممكن أن يكون ناتج الطرف الأيمن وهو ثلث (حيث البسط هو ثلث المقام) يساوي الطرف الأيسر وهو 3 !!! وعليه فإن مجموعة الحل خالية).
وأما الإجابة عن المسألة الثالثة والتي تعكس وجود الحس الرمزي تتمثل بـ (قيمة س = 1 لأن ناتج الطرف الأيمن يساوي 7 وعليه فإن 21 تقسيم ماذا ينتج 7 ! لا بد أن المقام كله يساوي 3 وبهذا يكون الكسر في المقام قيمته 1 وعليه فإن قيمة س ستكون 1).
المقصود مما سبق هو الإشارة إلى أنه وإن كان من الممكن ببساطة حل المهمة بتنفيذ الاجراءات، إلا أننا نتساءل: من منا كمعلمين يتيح لطلبته وقتا ليتأمل في المسألة ويتذوقها قبل الشروع بالحل الاجرائي! وكيف نرجو لطلبتنا أن يمتلكوا حسا رمزيا ونحن نغيبهم عن الشعور بالرموز بمهماتنا الروتينية! مع الإشارة بأن مراحل بناء الحس الرمزي لدى طلبة ذوي عسر التعلم تتطلب منا التجاوز شيئا عن لغتهم التعبيرية بإحساسهم بالرموز وتوجيههم شيئا فشيئا عبر الجلسات التعليمية والمهمات الرياضية إلى اللغة الرسمية الصحيحة.
المهمات التقويمية
المهمة الأولى (وتقيس مدى تحقق نتاجات المرحلة التمهيدية الأولى وتقدم للطلبة في مجموعات)
كم عدد الأشخاص الذين سيجلسون على س من الطاولات كما في الشكل الآتي:

المهمة الثانية (وتقيس مدى تحقق نتاجات المرحلة التمهيدية وتقدم لكل طالب بشكل فردي)
لدى أحمد وعلي حسابات على الانستغرام، يوجد 9 صور في أنستغرام أحمد، و3 صور في أنستغرام علي، وبدءا من الأسبوع الأول سينشر أحمد بانتظام صورتين أسبوعيا أما علي فسينشر 3 صور أسبوعيا. ما عدد الأسابيع اللازمة لجعل عدد الصور على أنستغرام أحمد هو نفسه لعلي؟
المهمة الثالثة (وتقيس قدرة الطالب على اختيار الرموز / مهمة فردية)
ماذا يمكننا القول عن ناتج طرح أي عدد فردي من مربعه؟
المهمة الرابعة (وتقيس مهارة التخلي عن الرموز لدى الطلبة واللجوء للتمثيل الهندسي/مهمة فردية)
ما قيمة ب التي تجعل للنظام الآتي حلان؟ (Cai & Knuth,2011)
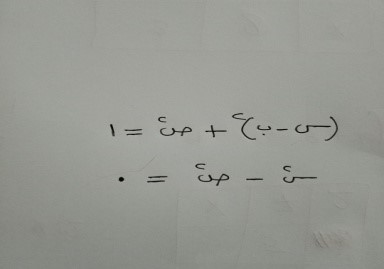
المهمة الخامسة (وتقيس مدى تحقق نتاجات المرحلة الثالثة / مهمة فردية)
دون استخدام القلم والورقة أوجد قيمة س في كل مما يلي:
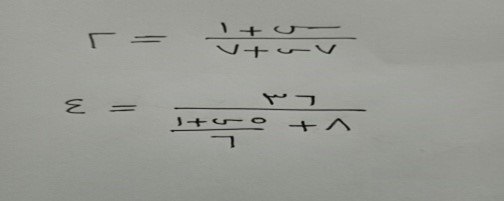
المراجع
Arcavi,Abraham.(1994). Symbol Sense: Informal Sense-making in Formal Mathematics.FLM Publishing Association,14(3).
Cai,J.&Knuth,E.(2011). Early Algebraization.Springer,London
Septiani,y.,Maudy,S.,&Endang,M. (2018). Student Algebraic Thinking Level .International Journal Of Information and Education Technology. 8 (9),672-676.
 تعليم جديد أخبار و أفكار تقنيات التعليم
تعليم جديد أخبار و أفكار تقنيات التعليم








رائع…
تسلمي مرورك الأروع
انا ممنونة لهذ الموقع جزيل الشكر لكل باحث افادني ببمعلومة تربوية كانت ام علمية ادعو الله لكم ا الفلاح و التوفيق
نشكر مرورك الكريم